Dalil/Teorema Menelaus pada segitiga

Materi Matematika

Pada postingan kali ini saya ingin berbagi tentang "Teorema Menelaus" pada materi geometri yang barang kali menjadi pokok bahasan pada Matematika Peminatan kelas x.

Dalam materi geometri, Teorema Menelaus (Menelaus’s Theorem) atau kadang disebut sebagai Dalil Menelaus, adalah teorema yang menjelaskan keterkaitan panjang sisi segitiga yang dipotong oleh segmen garis dan tiga titik yang segaris (kolinear) dengan menggunakan konsep perbandingan.

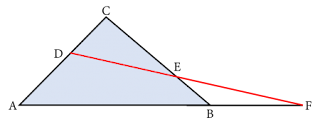
Diberikan segitiga sembarang $ABC.$ Titik $D$ terletak pada sisi $AC,$ sedangkan titik $E$ terletak pada sisi $BC.$ Titik $D$ dan $E$ dihubungkan dengan menggunakan garis lurus. $DE$ dan $AB$ diperpanjang sehingga berpotongan di titik $F$. Garis $DEF$ disebut transversal karena memotong dua garis, seperti yang tampak pada gambar berikut.

Teorema Menelaus menyatakan bahwa:

Titik $D, E,$ dan $F$ kolinear (segaris) jika dan hanya jika $$\dfrac{BE}{EC} \cdot \dfrac{CD}{DA} \cdot \dfrac{AF}{FB} = 1.$$

Penjelasan tambahan:

Untuk memudahkan dalam mengingat, alur panah seperti berikut kadang dapat menjadi solusi.

Alur menentukan perbandingan Menelaus

Source: dzulcyber.com